公众号开张的第一篇写了不确定性，过去的一年，时不时会再冒出这个话题来，因为它实在是太常见，又太重要了。比如这周全球热议的美国大选，就是个典型的案例。戏剧般变化的选情，以及特朗普政策本身的不确定性，无不牵动着全球股市的变化。两位候选人自己也是一脸蒙逼，希拉里不得不取消早早预备的庆功宴，而她其实有更好的选择，就是转让给特朗普，因为后者压根没有准备庆功宴。

今天从另一个角度再聊聊不确定性，算是对一年前的呼应。

Weinberg在《系统化思维导论》一书中用随机程度和复杂程度两个维度界定问题。这是一个全局的视角，让我一下子从细分的学科中跳出来，看清全貌。有了更加泛化和统一的框架来规整散落的学科认识，这是让我觉得受用的地方。“有序的简单”，是整个学生生涯的主要学习对象，如牛顿三大定律，质能方程等等。“无序的复杂”，问题本身可简单可复杂，但都表现出足够的随机性，因此可以进行统计研究，一个简单的例子：掷骰子，我们无法知道单次掷出的点数，但大量重复后又表现出一定规律。

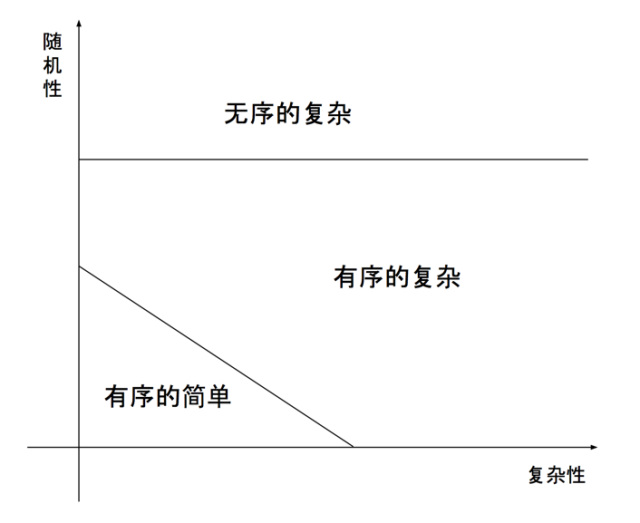
“有序的复杂”，是大自然中的普遍现象。这些现象，既不能用解析法准确分析，也不能用统计法预测概率，是不确定性的最大来源。

“一只南美洲亚马逊河流域热带雨林中的蝴蝶，偶尔扇动几下翅膀，可以在两周以后引起美国得克萨斯州的一场龙卷风”，这是大家熟知的蝴蝶效应。像这样演变过程对初态非常敏感的系统，称为混沌系统。

高晓松在最新一期《晓松奇谈》中反思美国大选，他提到在一个剧本里的假设：“每个人脑门上都直接显示内心的真实想法”，他预计世界人口会因此减少一半，然后重新稳定。因为，当一对男女互相说我爱你时脑门上却显示另一个人的名字，会起杀人的心思，政客说希望和贵国世代友好时脑门上却显示他只是来骗钱，也会引发战争的念头。

这是他的剧本，怎么构思他说了算。但他也许不知道，这个假设背后涉及了不确定性。

可以用马尔萨斯的“人口论”来研究这个假设，“人口论”背后的公式非常简单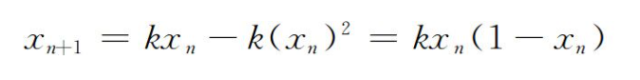： Xn表示第n代的人口相对于地球能承受的最大人口数N的比例 。这个公式综合考虑了人口增长率和诸如食物、疾病、战争，以及“脑门上装显示器”等因素对人口的影响。简单背后的复杂可能超出大部分人的估计。

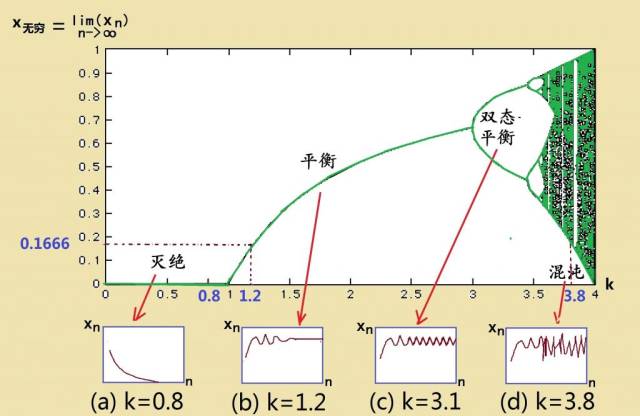
上图绿色曲线表示不同k值下繁衍到无穷后的情况，不同的初值k，最终的归宿截然不同，图中从左到右分别经历了灭绝、平衡、双态平衡和混沌。混沌状态时，人口不会收敛到稳定状态，而是在无穷多个不同的数值中无规则地跳来跳去。

这么看，高晓松大概把k值设定在1.2-2之间了。

知道了混沌现在后，我们还想进一步描述混沌的程度，于是就出现了“熵”的概念：一个系统混乱程度、或称无组织程度的度量。系统越混乱，熵就越大；系统越有序，熵就越小。不同熵值对人们做决策有什么影响呢？这在一年前的文章中有过讨论，可以翻出来看看。