像代数推导一般
2018-10-29
In math we trust——张首晟
纯函数已然为函数式编程赢得了巨大优势,但这还不够。纯函数还只是一块基石,它和另一块基础——数据不可变,一道构筑了函数式编程蔚为壮观的独特风景:代数推导。这是函数式编程最吸引我的地方,因为,数学终于从编程语言或者计算机科学的背后走向前台,让我们可以像代数推导一般,进行现实问题的建模和编码。根据张首晟教授的说法,区块链的信任机制本质上是对数学的信任。我想,这一样适用于函数式编程,数学的严谨性让模型和代码质量有了更多保障。而数学的抽象,让貌似不同的事物有了变成一样的可能,提高了代码的普适性。
学习函数式编程,与其说是学习某门具体的语言,不如说是学习如何运用代数结构描述现实事物,运用代数式子表达现实逻辑,运用代数推导求解现实问题。
面向表达式语言
代数,简而言之,研究的是:
- 对象的集合,这里的对象不是编程语言里的对象,反倒是更像类型。
- 用对象创建新对象的操作。
如,数构成集合,加减乘除构成操作。
介绍纯函数时,我们知道了数学上的运算可以写成纯函数,如f(x) = 2 * x + 3可以写成def f(x: Int) = x * x + 3,f(x, y) = x + y写成def f(x: Int, y: Int) = x + y。
集合里的对象,也就是语言的类型,后面再辟专门的章节讲述。先看看看代数的推导过程,蕴含了哪些值得借鉴的做法。以下是一道简单代数题的求解过程:
已知函数f(x + 2) = 2x^2 - 5x + 1,求f(x)。
解:
设 t = x + 2, 则x = t - 2
∴ f(t) = 2 * (t - 2)^2 - 5 * (t - 2) + 1
∴ f(t) = 2 * (t^2 - 4 * t + 4) - 5 * t + 10 + 1
∴ f(t) = 2 * t^2 - 13 * t + 19
即,f(x) = 2 * x^2 - 13 * x + 19
可以发现:
- 首先,在整个推导过程中,保持变量含义的不变,从头到尾的一致性。不会突然令
x = 9或别的值,当需要表达其它量时,启用新的变量t,并表述清楚t的来源t = x + 2,而不是复用原来的变量:x = x + 2。
有人把变量的不可变性视为函数式编程最重要的特性,因为,就像上述推导一样,它喻示着过程的可省视性。仅仅通过阅读代码,就可以理解整个逻辑,而不是指令式编程那样,必须在脑子里”运行”代码。当大脑无法跟踪太多变量的变化时,不得不借用纸笔或调试工具来debug,只消几层的if判断就足以把人绕晕。有了不可变性,可以放心地将代码的各个部分分离开,独立解读,脑子里要保留、跟踪的信息几乎不随代码规模的增长而增加。
- 其次,在值相同的情况下,符号和表达式可以互相替代,如
t和x + 2在通篇任意位置可以互相替代,这种替代在数学上叫换元,用于辅助推导,并不改变语义。
若要在代码层面“换元”,则要求满足引用透明,引用透明辅助编译器对代码做优化,如果没有引用透明,编译器无法自由地替换“表达式“和“值”,因为前后两次的执行结果可能不同,哪怕结果完全一样,程序只能无奈地一次次对该表达式做求值操作。也不能改变表达式的顺序,因为前后两次的求值结果可能不一样,进而限制了程序的并发性。
代数也是一门语言,它用数学模型描述现实世界,并解决逻辑问题。如果把它也看成一门编程语言,它应该归入什么类别呢?大概“面向表达式语言”是比较合理的分类。没错,表达式!看上面代数题的求解过程,本质是表达式的归约操作、合并同类项操作。所谓归约,就是将每个最内层可归约表达式用其值来替换,这样又形成了新的最内层可归约表达式,然后再对其进行归约,最后,整个程序全部被归约,仅留下最终结果。
所以,用它解决问题的过程应该是,用数字或符号描述现实世界,如直角三角形的两和直角边长度分别为a和b,依据放之四海而皆准的公理,如勾股定理,构建它们的逻辑关系,如斜边c^2 = a^2 + b^2
,再用加减乘除等运算操作,简化、规约表达式,求得斜边长度。这一过程中,我们并没有过问这些变量寄存在哪里(有人直接在脑子里算,也有人要在纸上演算),也不关心它们是否复用了同一块内存,会不会被其它人错误地读写了。我们关心的是想要什么,得到结果的逻辑是什么,而不是如何赋值、如何改写变量。前者是人类擅长的,后者是机器擅长的。我们应让机器服务人类,而不是反过来,人类迁就机器。为此,我们需要一个工具,把高阶的人类思维忠实地转换为低阶的机器语言。
函数式语言就是这样的工具,它有一个少为人知的别名,正是“面向表达式语言”。表达式是值和逻辑(函数)的组合,讲究如何编织逻辑以创建新的值,执行的过程即是规约化得到最终结果的过程,如:val total = sum(list),sum是一个求和的运算逻辑,通过这个逻辑得到值sum。 与之相反的是指令式,用一系列的执行单元,告诉计算机如何改变指令计数器、数据存储器、当前计数状态等,通过状态的改变得到最终结果,如:list.sum(),sum是个运算指令,它不返回计算的值,而是改变了某个状态,通过读取这个状态的地址得到结果。
指令式语言让我们从低级语言的内存、栈、寄存器等概念中解脱,却依然是指令运行过程的封装:循环、锁、线程、并发。函数式语言则进一步抽象,更多地让编译器、解析器处理这些概念,让人腾出更多精力关注数据模型、关注业务逻辑。
函数的组合
他山之石,可以攻玉。我们回头再挖掘下代数里可以借鉴的特质。
如果f(x)=3x-1,且g(x)=x^3+2,那么f(g(3))的值是多少?
间接的做法是,先求得g(3) = 29,进而f(g(3)) = f(29) = 86。那么,有没有直接的做法呢?
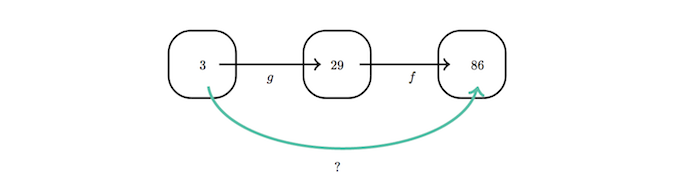
为了直接计算f(g(x)),我们得组合(Composition)f和g这两个函数。由于g(x)是f(x)的输入,可以把f(x)的各个x替换为g(x),得到f(g(x)) = 3g(x)-1 = 3x^3+5,即是图中绿线所表示的函数。
在Scala里,Function1接口定义了compose方法和andThen方法,均可以用来组合单参数函数。f(g(x))可以写成:
def f(s: String): String = "f: " + s
def g(s: String): String = "g: " + s
def fg = f _ compose g
def fg2 = g _ andThen f
注意,”_“表示Eta expansion。
组合看上去再自然不过了,以至于我们不觉得有什么特别或厉害的。然而,稀松平常的组合却透露了编程的本质。
我们是如何解决问题的?每当碰到复杂的问题,就把它分解为更小的问题,直到问题足够小,小到我们可以写代码解决它。然后,再组合这些小颗粒度的代码,形成原始问题的解决方案。问题规模的限制并不是计算机强加给我们的,而是人类大脑的限制。1956年发表的著名论文《神奇的数字 7,加减 2:人类信息加工容量的某些局限》指出,不管记忆的内容怎么变化,是数字,字母,数字 + 字母,还是从 1000 个单音节单词中随机选,人们在记忆这些材料的时候,大概只能记住 5-9 个。所以,我们必须把一次性可以处理的代码块规模控制在大脑可以接受的程度。所谓”优雅代码”,不是结构清晰、简洁所能概括的,更切中要害的说法是,可被有限的大脑带宽处理。
分解本身不是目的,解决问题需要重组这些子块,如果无法重新组合,分解的意义就不存在。什么样的函数能组合呢?显然,一个函数的输出类型必须和另一个函数的输入类型保持一致。至少在函数式语言内,这是”类型”概念存在的根本原因。有关类型,我们后面再详谈。
微信扫一扫
