默克尔树(Merkle Tree)
2018-07-08
默克尔树(Merkle Tree)的定义很简单,却是区块链技术领域的重要概念。它使得大规模的分布式区块网络成为可能,也让普通机器可以成为网络节点。
什么是默克尔树
数据结构上,它是一种特殊的二叉树(也可以是多叉树),设计如下:
- 叶子节点的值是数据的哈希值。
- 非叶子节点的值是其所有子节点的哈希值。
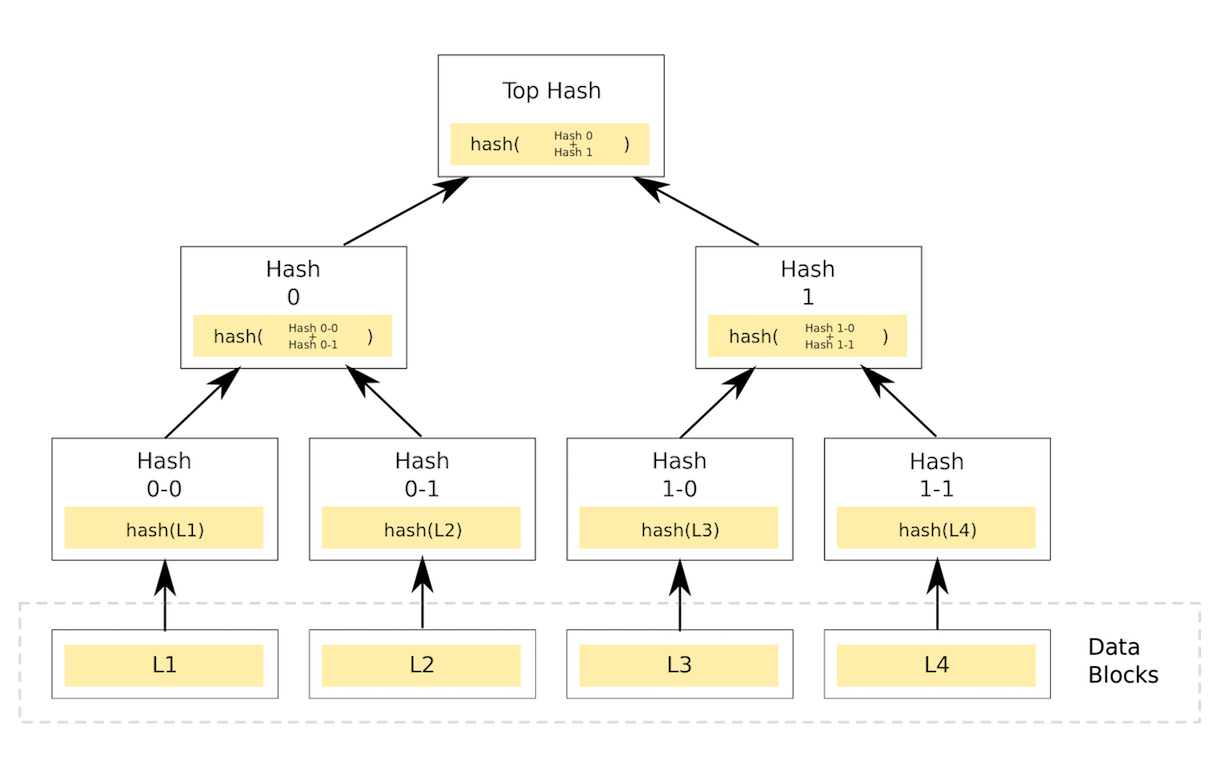
如上图所示,
- hash代表哈希算法,如MD5,SHA系列等,可把任意长度的数据转换为固定长度的哈希值。
- L1, L2等是叶子节点对应的数据,直接作为哈希算法的输入。
- 非叶子节点的哈希输入为所有对应子节点哈希串的拼接。
- 最终形成唯一的根节点,称为默克尔根(Merkle Root).
上图叶子节点数为4,恰好每一层都有完整输入。如果叶子节点数量不是2的次方,即不能形成满二叉树,怎么处理呢?
有多种处理“孤立”叶子节点的方式。一种方案是不断重复最后一个节点,直到整体数量达到2^n 个。这种方案的想法比较直接,缺点也很明显,多做了很多无用功。比较好的方法是,把“孤立”节点提升到更高层次中。具体提到哪一层,要看叶子节点的数量情况,下图展示了5-7个叶子节点的情况:
┌───┴──┐ ┌────┴───┐ ┌─────┴─────┐
┌──┴──┐ │ ┌──┴──┐ │ ┌──┴──┐ ┌──┴──┐
┌─┴─┐ ┌─┴─┐ │ ┌─┴─┐ ┌─┴─┐ ┌─┴─┐ ┌─┴─┐ ┌─┴─┐ ┌─┴─┐ │
(5) (6) (7)
默克尔树的特性
-
对变动敏感。任何细微的变动都会引发叶子节点哈希值的变化,依次向上传导,最终导致根节点的变动。因此,像普通哈希一样,可以用来验证数据拷贝的一致性。
-
快速定位差异。二叉树查询的时间复杂度为O(logN),沿着根节点向下对比,可以非常高效地确定具体是哪个(些)叶子的数据有差异。
-
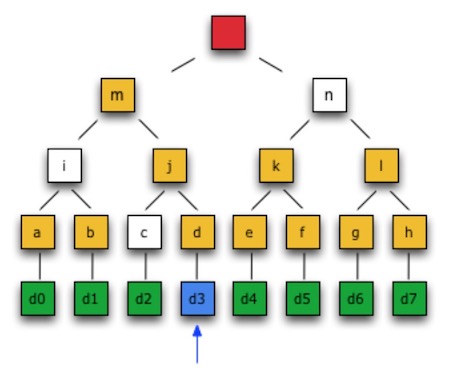
默克尔证明。如图,要证明数据d3在数据集中,只要知道节点c,i,n(白色节点)的值,即可通过重新计算节点d,j,m的值,进而计算根节点的值,再和给定的根节点对比,判断d3是否属于该数据集。不需要拿到所有数据,即可完成此验证。
默克尔树的应用
P2P下载
在p2p下载出现之前,整个文件的数据都从一个中心节点上获取。这个中心节点的资源和稳定性常常成为瓶颈点,一旦下载异常,整体文件都需要重新下载。p2p 网络出现后,一个大文件被分割成许多小块,编号后分布在不同的资源节点上,下载操作同时从多个节点上进行,每一块都有对应的哈希值,用于下载后的检验。就算一个块出错,只需要重新下载这小块就行,而不需要重新下载整个文件。
问题是如何确保每一块的哈希值本身是正确的呢,在p2p 网络中,任何人都可以成为提供下载资源的节点,无法确保数据本身或其哈希值没被恶意修改。一种方式是由可靠的权威节点提供这些小块数据的哈希值,可以从做任意节点下载资源,但只从权威节点下载哈希值。这当然可行,但对权威节点的依赖还是太大了。
默克尔树能解决这个问题呢?把小块数据作为叶子节点,构建默克尔树,只要根节点的哈希值从可信节点下载,剩下所有数据和节点哈希值都可以从任意节点下载。各个分支的值可以对其子树进行检测,根的值则可以对整个默克尔树进行检测。这样既可以各个分支并行独立处理,又确保了整个大文件的完整性。
比特币交易验证
比特币的设计里,区块头是不包含交易(Transaction)信息的,关于交易的数据只是交易构建的默克尔树的根节点。
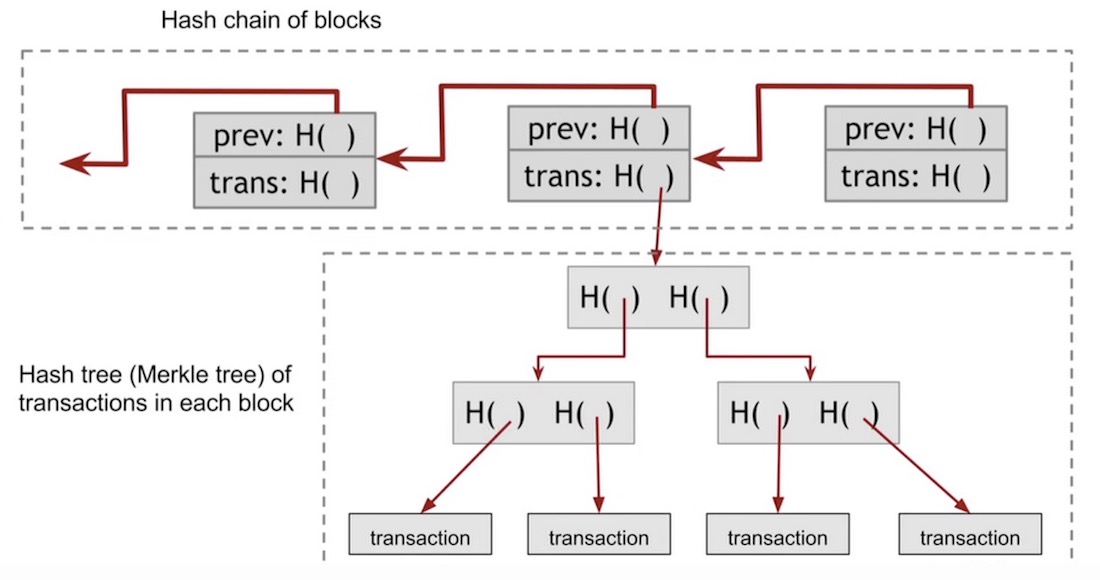
而比特币网络的轻量客户端(如钱包)又不存储完整的区块数据,仅下载区块头,就能验证某笔交易是否被打包到链上。这是如何做到的呢?客户端验证步骤如下:
- 首先对交易数据进行哈希。
- 然后咨询完整节点:这个哈希值对应的交易是否在第index 个区块中?
- 完整节点的区块不会直接返回在或不在的结论,而是返回一个默克尔证明(重新计算根节点所需的路径)。
- 客户端验证这个”默克尔证明”,即独立计算根节点的哈希值。
- 对比区块头中的哈希值与计算结果是否相同。
对于n笔交易而言,路径节点数只要log2(n),无论是查找还是数据传输都是一个巨大的效率提升。不妨试算一下,假设某个区块包含32768笔交易,每笔交易占256字节,则所有交易大小为8M ,而路径数为15,每个哈希占32字节,则路径大小仅为480字节,差距高达5个数量级。
值得指出的是,比特币网络的任何节点都不会也没必要相信其它节点,节点只能依赖事先约定的协议独立地验证来自网络的数据。这个验证的最终基础正是数学。用张首晟的话说:
In math, we trust.
当然,默克尔树早在比特币之前就已经广泛使用了,分布式代码版本工具Git,以及开源数据库Apache Cassandra均有使用。
默克尔树的实现
为了加深理解,用python实现了简单的默克尔树,包含构建、验证和查找功能。数据结构本身比较清楚明了,关键代码做了注释,这里不再讨论。可直接到github阅读源码。
参考文档
- https://github.com/adjoint-io/merkle-tree
- https://en.wikipedia.org/wiki/Merkle_tree
- https://brilliant.org/wiki/merkle-tree/
- https://juejin.im/entry/5a2e1135f265da432f311168
微信扫一扫
